The deployment of machine learning models in production environments requires rigorous validation through controlled experimentation, and A/B testing has emerged as the gold standard for evaluating AI system performance in real-world conditions. Understanding how to properly design, execute, and analyze A/B tests for machine learning models is crucial for data scientists and AI engineers who need to make evidence-based decisions about model deployments while ensuring statistical validity and business impact.
Explore the latest AI testing methodologies to stay informed about cutting-edge approaches to model validation and experimental design in the rapidly evolving artificial intelligence landscape. The intersection of statistical rigor and machine learning deployment represents a critical competency that separates successful AI implementations from those that fail to deliver measurable business value.
Fundamentals of A/B Testing in Machine Learning
A/B testing for machine learning models extends beyond traditional web optimization experiments by incorporating the complexities of model behavior, prediction accuracy, and algorithmic decision-making into the experimental framework. Unlike simple interface changes that can be evaluated through conversion rates or click-through metrics, machine learning A/B tests must account for model performance variations, prediction confidence intervals, and the temporal dynamics of learning systems that may adapt over time.
The fundamental principle underlying ML A/B testing involves comparing the performance of two or more model variants under identical conditions while controlling for external factors that could influence outcomes. This approach requires careful consideration of sample size calculations, randomization strategies, and statistical power analysis to ensure that observed differences between models represent genuine performance improvements rather than random fluctuations in the data.
The complexity of machine learning A/B testing stems from the multifaceted nature of model evaluation metrics, which may include accuracy, precision, recall, F1-scores, area under the curve, mean squared error, and business-specific key performance indicators. Each metric requires separate statistical analysis, and the interpretation of results must consider the trade-offs between different performance dimensions and their relative importance to the business objectives.
Statistical Foundations for ML Experimentation
Statistical significance in machine learning experiments requires a deep understanding of hypothesis testing, confidence intervals, and the assumptions underlying various statistical tests. The null hypothesis in ML A/B testing typically states that there is no difference between the performance of competing models, while the alternative hypothesis suggests that one model significantly outperforms another according to predefined metrics and business criteria.
The choice of statistical test depends on the nature of the evaluation metric and the distribution of the underlying data. For binary classification problems, chi-square tests or Fisher’s exact tests may be appropriate for comparing error rates, while continuous metrics like mean squared error or log-likelihood require t-tests or non-parametric alternatives like the Mann-Whitney U test when normality assumptions are violated.
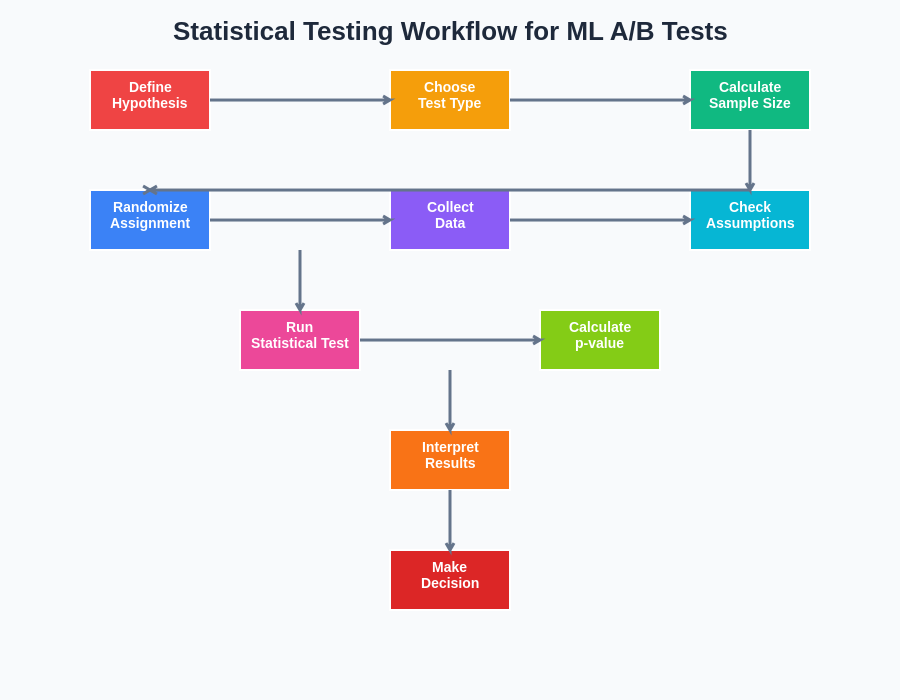
The systematic approach to statistical testing in machine learning experiments requires careful adherence to established protocols that ensure valid inference and reproducible results. This workflow emphasizes the importance of pre-planning experimental design decisions and maintaining rigorous standards throughout the testing process.
Enhance your statistical analysis with advanced AI tools like Claude that can help design robust experimental frameworks and interpret complex statistical results in the context of machine learning model evaluation. The integration of AI-powered analysis tools with traditional statistical methods creates opportunities for more sophisticated and nuanced experimental designs.
Power analysis plays a crucial role in determining appropriate sample sizes for machine learning A/B tests, as underpowered experiments may fail to detect meaningful differences between models, while overpowered tests may identify statistically significant but practically irrelevant improvements. The calculation of statistical power must account for effect size expectations, significance level requirements, and the inherent variability in model predictions across different segments of the population.
Experimental Design for Model Comparison
Effective experimental design for machine learning A/B tests requires careful consideration of randomization strategies, stratification approaches, and control mechanisms that ensure fair comparison between competing models. Random assignment of users or data points to different model variants must be implemented in a way that prevents selection bias while maintaining the independence assumption required for valid statistical inference.
Stratified randomization becomes particularly important in machine learning experiments where population heterogeneity could significantly impact model performance. By ensuring balanced representation of key demographic groups, geographic regions, or behavioral segments across experimental conditions, researchers can improve the precision of their estimates and enhance the generalizability of their findings to the broader population.
The temporal aspects of machine learning A/B testing present unique challenges that require sophisticated experimental designs capable of handling time-varying effects, seasonal patterns, and concept drift. Sequential testing methodologies and adaptive experimental designs offer solutions for managing these complexities while maintaining statistical rigor and enabling early stopping when clear winners emerge from the comparison.
Metrics Selection and Statistical Validation
The selection of appropriate evaluation metrics for machine learning A/B tests requires alignment between technical model performance indicators and business outcomes that drive organizational decision-making. Primary metrics should directly reflect the business objectives that motivated the model development effort, while secondary metrics provide additional context about model behavior and potential unintended consequences.
Statistical validation of chosen metrics involves verifying that the measurement systems accurately capture the intended phenomena and that the metrics demonstrate sufficient sensitivity to detect meaningful differences between model variants. This validation process may include correlation analysis between technical metrics and business outcomes, stability testing across different time periods, and sensitivity analysis to understand how metric values respond to known changes in model performance.
The multiple testing problem becomes particularly acute in machine learning A/B tests where researchers may evaluate dozens of metrics across various population segments and time periods. Proper adjustment for multiple comparisons using methods like Bonferroni correction, false discovery rate control, or family-wise error rate management ensures that the overall Type I error rate remains within acceptable bounds while preserving the ability to detect genuine improvements.
Sample Size Calculation and Power Analysis
Determining appropriate sample sizes for machine learning A/B tests requires sophisticated calculations that account for the specific characteristics of the evaluation metrics, expected effect sizes, and desired levels of statistical power. The traditional sample size formulas must be adapted to handle the unique properties of machine learning metrics, such as the discrete nature of classification accuracy or the potentially non-normal distributions of regression residuals.
Effect size estimation presents a particular challenge in machine learning experimentation, as the practical significance of metric improvements may not align with statistical significance thresholds. A one percent improvement in model accuracy might be highly valuable in a high-stakes application like medical diagnosis, while the same improvement might be negligible in a recommendation system context where user satisfaction depends on factors beyond prediction accuracy.
Leverage advanced research capabilities with Perplexity to access the latest academic research on statistical methods for machine learning experimentation and stay current with evolving best practices in the field. The rapid advancement of statistical methodologies specifically designed for AI applications requires continuous learning and adaptation of experimental approaches.
Sequential analysis and adaptive sample size determination offer alternatives to fixed sample size calculations by allowing researchers to monitor accumulating evidence and adjust experiment parameters based on observed effect sizes and variance estimates. These approaches can improve experimental efficiency by enabling early termination when sufficient evidence has been gathered, while maintaining strict control over Type I and Type II error rates.
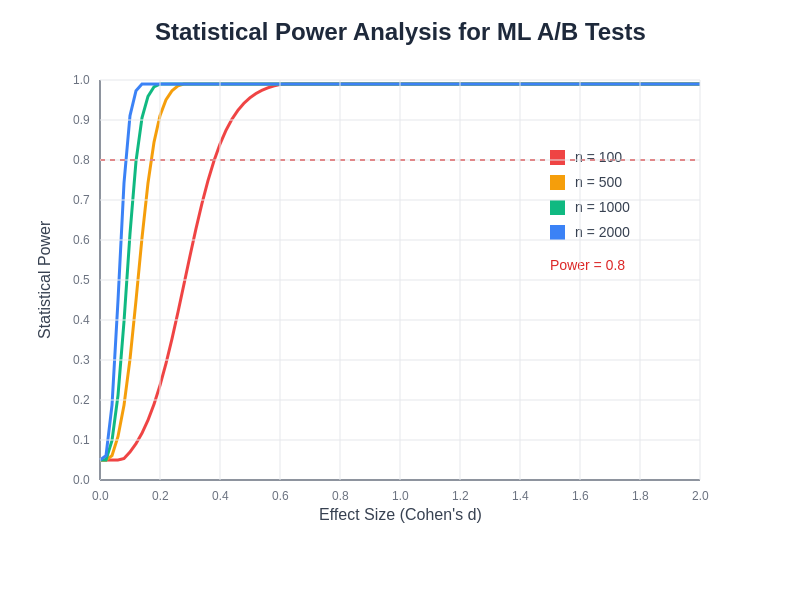
Understanding the relationship between effect size, sample size, and statistical power is fundamental to designing effective machine learning experiments. The power curves demonstrate how larger sample sizes enable detection of smaller effect sizes, while the conventional power threshold of 0.8 provides a practical guideline for experimental planning.
Randomization Strategies and Bias Prevention
Proper randomization in machine learning A/B tests extends beyond simple random assignment to include sophisticated strategies for handling clustered data, temporal dependencies, and the potential for interference between experimental units. The independence assumption underlying most statistical tests can be violated when users interact with each other or when model predictions influence future data generation processes.
Cluster randomization becomes necessary when the experimental units are naturally grouped, such as when testing recommendation algorithms where household members may influence each other’s behavior, or when evaluating fraud detection systems where fraudulent activities may occur in coordinated patterns. The statistical analysis must account for intra-cluster correlation to avoid inflated Type I error rates and incorrect conclusions about model performance.
Switchback experiments and time-based randomization strategies address temporal dependencies and carryover effects that can contaminate traditional A/B test results in machine learning applications. These designs alternate between different model variants over time while accounting for trends, seasonality, and learning effects that may influence the apparent performance of competing algorithms.
Handling Non-Stationary Environments
Machine learning models often operate in non-stationary environments where the underlying data distribution changes over time, presenting unique challenges for A/B testing methodologies that assume stable experimental conditions. Concept drift, seasonal variations, and external shocks can significantly impact model performance and complicate the interpretation of experimental results.
Adaptive experimentation frameworks provide solutions for managing non-stationary environments by incorporating change detection mechanisms, dynamic rebalancing of experimental assignments, and statistical methods that account for time-varying effects. These approaches enable researchers to distinguish between genuine model improvements and performance changes driven by environmental factors beyond the control of the experimental design.
The analysis of experiments in non-stationary environments requires sophisticated statistical techniques that can separate treatment effects from temporal trends while maintaining valid inference procedures. Time series analysis, change point detection, and regime-switching models offer methodological frameworks for handling these complexities while preserving the ability to draw reliable conclusions about relative model performance.
Business Impact Measurement and ROI Analysis
The ultimate success of machine learning A/B tests depends on their ability to demonstrate measurable business impact and justify the resources invested in model development and deployment. This requires translation of technical performance metrics into business outcomes such as revenue generation, cost reduction, customer satisfaction, or operational efficiency improvements.
Return on investment calculations for machine learning initiatives must account for both the direct costs of model development, infrastructure, and maintenance, as well as the opportunity costs of alternative approaches and the risk-adjusted value of performance improvements. The statistical uncertainty in performance estimates should be propagated through the ROI analysis to provide decision-makers with confidence intervals around expected business benefits.
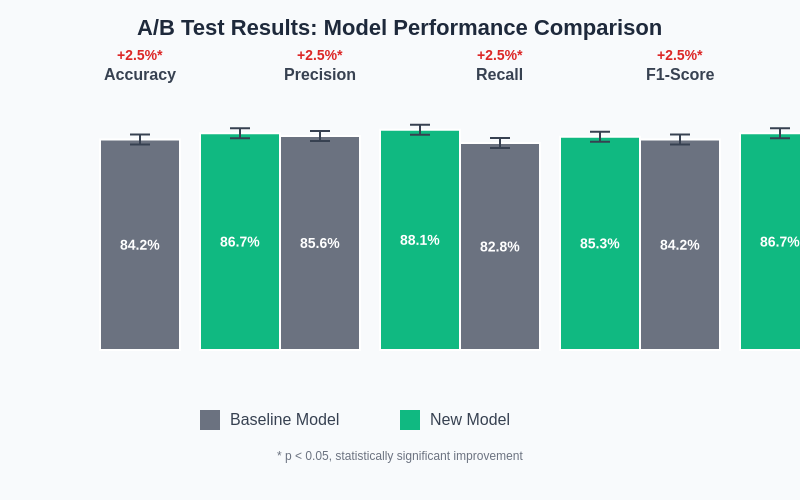
The presentation of A/B test results requires clear visualization of performance differences, confidence intervals, and statistical significance indicators. This comprehensive comparison demonstrates how new models can achieve meaningful improvements across multiple evaluation metrics while maintaining statistical rigor in the analysis.
Long-term impact assessment requires extended observation periods and sophisticated causal inference techniques that can distinguish between immediate treatment effects and sustained performance improvements. This longitudinal analysis helps organizations understand the durability of model improvements and make informed decisions about ongoing investment in AI capabilities.
Advanced Statistical Techniques for ML A/B Testing
Modern machine learning A/B testing benefits from advanced statistical techniques that address the unique challenges of algorithmic experimentation while providing more nuanced insights into model behavior. Bayesian experimental design offers advantages over traditional frequentist approaches by incorporating prior knowledge about model performance, enabling more flexible stopping criteria, and providing probabilistic interpretations of results that align with business decision-making processes.
Multi-armed bandit algorithms represent an evolution beyond traditional A/B testing by dynamically allocating traffic to better-performing model variants while continuing to gather evidence about relative performance. These approaches optimize the trade-off between exploration and exploitation, potentially reducing the opportunity cost of experimentation while maintaining statistical rigor in the evaluation process.
Causal inference methods such as propensity score matching, instrumental variable analysis, and difference-in-differences designs provide additional tools for evaluating machine learning models in observational settings where randomized experiments may not be feasible. These techniques help researchers account for selection bias, confounding variables, and other threats to valid causal inference in complex real-world environments.
Implementation Best Practices and Common Pitfalls
Successful implementation of machine learning A/B tests requires attention to numerous technical and organizational details that can significantly impact the validity and utility of experimental results. Data quality issues, instrumentation problems, and implementation bugs can introduce systematic biases that undermine the entire experimental effort, making careful quality assurance and validation procedures essential components of the testing process.
Common pitfalls in ML A/B testing include inadequate randomization procedures, insufficient sample sizes, multiple testing without proper correction, and misinterpretation of statistical significance in the context of practical significance. These issues can lead to incorrect conclusions about model performance and poor decision-making regarding model deployment and resource allocation.
Organizational challenges such as stakeholder alignment, communication of statistical concepts to non-technical audiences, and integration of experimental results into product development cycles require careful management to ensure that A/B testing efforts contribute effectively to business objectives. Clear documentation, standardized procedures, and cross-functional collaboration help maximize the value of experimental investments.
Future Directions in ML Experimentation
The field of machine learning experimentation continues to evolve with advances in statistical methodology, computational capabilities, and understanding of algorithmic behavior in complex environments. Automated experimentation platforms, AI-powered experimental design, and real-time adaptive testing represent emerging trends that promise to improve the efficiency and effectiveness of model evaluation processes.
The integration of machine learning with experimental design itself creates opportunities for more sophisticated and personalized experimentation approaches that can adapt to individual user characteristics, temporal patterns, and contextual factors. These meta-learning approaches may enable more efficient discovery of optimal model configurations while reducing the time and resources required for comprehensive evaluation.
As machine learning systems become more complex and interconnected, the development of experimental methodologies that can handle system-level effects, network dependencies, and emergent behaviors will become increasingly important for ensuring the reliable deployment of AI technologies in production environments.
Disclaimer
This article provides general guidance on statistical methods for machine learning experimentation and should not be considered as professional statistical consulting advice. The specific requirements for experimental design and analysis may vary significantly depending on the application domain, regulatory environment, and business context. Readers should consult with qualified statisticians and domain experts when designing critical experiments that will inform major business decisions or regulatory submissions.
