The intersection of functional programming and artificial intelligence represents one of the most intellectually stimulating and mathematically rigorous approaches to machine learning development. Haskell, with its pure functional paradigm, lazy evaluation, and sophisticated type system, offers a uniquely elegant framework for implementing machine learning algorithms that closely mirror their mathematical foundations. This mathematical approach to ML programming not only enhances code correctness and maintainability but also provides unprecedented clarity in expressing complex algorithmic concepts through the lens of mathematical abstraction.
Explore the latest AI programming trends to understand how functional programming languages are gaining traction in the machine learning community. The mathematical nature of Haskell’s approach to AI development creates a natural bridge between theoretical machine learning concepts and their practical implementation, resulting in code that reads like mathematical notation while maintaining the computational efficiency required for real-world applications.
The Mathematical Foundation of Functional AI
Haskell’s approach to machine learning programming is fundamentally rooted in mathematical principles that align perfectly with the theoretical underpinnings of artificial intelligence algorithms. The language’s emphasis on pure functions, immutable data structures, and referential transparency creates an environment where mathematical concepts can be expressed directly in code without the cognitive overhead of managing state mutations or side effects that plague imperative programming approaches.
The type system in Haskell serves as a powerful tool for encoding mathematical constraints and relationships directly into the program structure. This capability allows developers to leverage the compiler as a mathematical proof assistant, ensuring that algorithmic implementations respect the mathematical properties and invariants that define correct machine learning behavior. The result is code that not only functions correctly but also maintains mathematical integrity throughout complex transformations and computations.
Linear algebra operations, which form the backbone of most machine learning algorithms, can be expressed in Haskell with remarkable clarity and safety. The type system ensures dimensional compatibility in matrix operations, preventing common errors that frequently occur in imperative implementations. Function composition naturally mirrors mathematical function composition, allowing complex algorithmic pipelines to be constructed through elegant combination of simpler mathematical operations.
Type Safety in Machine Learning Computations
The sophisticated type system that characterizes Haskell programming provides unprecedented safety guarantees for machine learning computations, where subtle errors can propagate through complex mathematical transformations and produce misleading results. Unlike dynamically typed languages commonly used in machine learning, Haskell’s static type checking catches dimensional mismatches, unit inconsistencies, and logical errors at compile time, significantly reducing the debugging burden associated with complex mathematical computations.
Phantom types and dependent typing capabilities in Haskell enable developers to encode mathematical properties such as matrix dimensions, probability distributions, and statistical assumptions directly into the type system. This approach ensures that operations respect mathematical constraints without runtime overhead, creating a programming environment where the compiler actively assists in maintaining mathematical correctness throughout the development process.
Discover advanced AI programming techniques with Claude to explore how type-safe functional programming can enhance your machine learning implementations. The combination of mathematical rigor and computational safety creates an ideal environment for developing reliable AI systems that can be formally verified and mathematically reasoned about.
Lazy Evaluation and Computational Efficiency
Haskell’s lazy evaluation strategy provides unique advantages for machine learning computations, particularly in scenarios involving large datasets, infinite data structures, and complex algorithmic pipelines. The ability to define infinite sequences and streams enables elegant implementations of iterative algorithms such as gradient descent, where convergence criteria can be naturally expressed as take operations on infinite sequences of parameter updates.
The lazy evaluation model also facilitates memory-efficient processing of large datasets by computing only the portions of data that are actually required for a given computation. This property is particularly valuable in machine learning contexts where dataset sizes often exceed available memory, and efficient streaming algorithms become essential for practical implementation.
Furthermore, lazy evaluation enables powerful optimization opportunities through fusion laws and deforestation techniques that can eliminate intermediate data structures in complex computational pipelines. These optimizations are particularly relevant in machine learning contexts where algorithmic efficiency directly impacts the feasibility of training and inference operations on large-scale problems.
Mathematical Abstractions and Algorithm Design
The mathematical abstractions available in Haskell provide a natural framework for expressing machine learning algorithms in terms of their underlying mathematical structures. Functors, applicative functors, and monads offer powerful abstraction mechanisms that can encapsulate common patterns in machine learning computations while maintaining mathematical transparency and composability.
Gradient-based optimization algorithms, for instance, can be naturally expressed using automatic differentiation libraries that leverage Haskell’s abstraction capabilities to provide seamless differentiation of arbitrary mathematical expressions. The mathematical elegance of this approach allows developers to focus on algorithmic design rather than the mechanical details of computing derivatives, resulting in more maintainable and mathematically transparent implementations.
Statistical computations and probabilistic programming benefit significantly from Haskell’s abstraction mechanisms, where probability distributions can be treated as first-class mathematical objects that compose naturally through monadic operations. This approach enables elegant implementations of Bayesian inference algorithms, Monte Carlo methods, and probabilistic machine learning models that closely mirror their mathematical specifications.
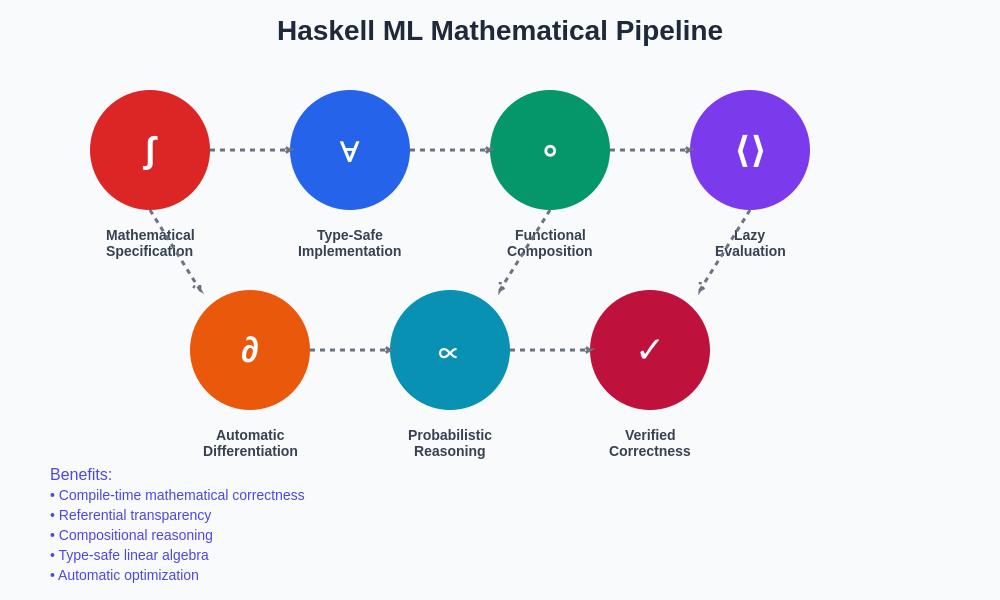
The mathematical pipeline approach in Haskell creates a seamless flow from theoretical foundations through implementation to practical application, where each transformation maintains mathematical rigor while building upon elegant functional abstractions.
Pure Functional Neural Networks
Neural network implementations in Haskell demonstrate the power of functional programming for expressing complex mathematical computations with clarity and safety. The pure functional approach to neural network design eliminates many of the subtle bugs associated with mutable state management in traditional imperative implementations while providing mathematical transparency that enhances understanding and debugging capabilities.
Backpropagation algorithms, which form the core of neural network training, can be implemented using automatic differentiation techniques that naturally arise from Haskell’s mathematical abstractions. The resulting implementations are not only more mathematically transparent but also more composable, allowing for easy experimentation with different network architectures and training algorithms without compromising mathematical correctness.
The type system ensures that network architectures are well-formed and that data flows through the network respect dimensional constraints. This compile-time verification eliminates entire classes of runtime errors that commonly occur in neural network implementations, particularly those related to dimensional mismatches and architectural inconsistencies.
Probabilistic Programming and Bayesian Inference
Haskell’s mathematical foundations make it particularly well-suited for probabilistic programming and Bayesian inference applications, where mathematical rigor and compositional reasoning are essential for correct implementation. The language’s abstraction mechanisms provide natural ways to represent probability distributions, conditional dependencies, and inference procedures as composable mathematical objects.
Markov Chain Monte Carlo algorithms, variational inference methods, and other Bayesian computation techniques can be implemented with remarkable mathematical clarity in Haskell. The pure functional nature of the language ensures that probabilistic computations maintain their mathematical properties while providing efficient implementations suitable for real-world applications.
The type system can encode important probabilistic properties such as normalization constraints, conditional independence assumptions, and sampling distributions, providing compile-time guarantees that probabilistic programs respect their mathematical foundations. This approach significantly reduces the likelihood of subtle errors that can compromise the validity of Bayesian inference procedures.
Linear Algebra and Numerical Computations
Linear algebra operations, which form the computational backbone of most machine learning algorithms, benefit tremendously from Haskell’s mathematical approach to programming. The language’s abstraction mechanisms allow for elegant implementations of matrix operations, eigenvalue computations, and numerical optimization procedures that closely mirror their mathematical definitions while maintaining computational efficiency.
Vector spaces, linear transformations, and other algebraic structures can be represented directly in Haskell’s type system, ensuring that operations respect mathematical constraints and relationships. This approach eliminates many common errors associated with linear algebra computations in imperative languages while providing a programming model that enhances mathematical understanding and algorithmic transparency.
Numerical stability considerations, which are crucial for reliable machine learning implementations, can be addressed through careful use of Haskell’s numeric type hierarchy and precision control mechanisms. The language’s mathematical foundations provide natural frameworks for implementing numerically robust algorithms that maintain accuracy across a wide range of computational scenarios.
Enhance your research capabilities with Perplexity to explore cutting-edge developments in functional programming approaches to machine learning and mathematical computation.
Domain-Specific Languages for Machine Learning
Haskell’s metaprogramming capabilities and abstraction mechanisms make it an ideal platform for developing domain-specific languages tailored to machine learning applications. These DSLs can provide specialized syntax and semantics that closely match the mathematical notation and conceptual frameworks used in specific machine learning domains while benefiting from Haskell’s type safety and mathematical foundations.
Embedded domain-specific languages for neural networks, probabilistic programming, and optimization can be designed to provide intuitive programming interfaces that hide implementation complexity while maintaining mathematical rigor. This approach enables domain experts to express algorithms using familiar mathematical notation while benefiting from the safety and efficiency provided by Haskell’s underlying infrastructure.
The composability of functional abstractions ensures that domain-specific languages can be combined and extended naturally, allowing for the development of comprehensive machine learning frameworks that support multiple algorithmic paradigms within a unified mathematical foundation.
Automatic Differentiation and Optimization
Automatic differentiation represents one of the most compelling applications of Haskell’s mathematical programming capabilities, where the language’s abstraction mechanisms enable transparent and efficient computation of derivatives for arbitrary mathematical expressions. This capability is fundamental to most modern machine learning algorithms, where gradient-based optimization drives both training and inference procedures.
Forward-mode and reverse-mode automatic differentiation can be implemented elegantly in Haskell using techniques such as dual numbers and continuation-passing style. These implementations provide exact derivatives without the numerical approximation errors associated with finite difference methods while maintaining the compositional properties that make complex algorithmic pipelines tractable and maintainable.
The mathematical transparency of automatic differentiation in Haskell enables developers to reason precisely about optimization procedures, convergence properties, and numerical stability characteristics. This level of mathematical control is particularly valuable for research applications where algorithmic innovation requires deep understanding of optimization dynamics and gradient flow behaviors.

The comparison between functional and imperative approaches to machine learning highlights the mathematical advantages and safety guarantees that functional programming brings to AI development, demonstrating superior outcomes in correctness, maintainability, and mathematical transparency.
Parallel and Concurrent Machine Learning
Haskell’s approach to parallelism and concurrency provides natural frameworks for implementing distributed machine learning algorithms that maintain mathematical correctness while exploiting computational resources efficiently. The pure functional nature of Haskell code eliminates race conditions and synchronization issues that commonly plague parallel imperative implementations, enabling straightforward parallelization of mathematically intensive computations.
Data parallelism, which is essential for processing large datasets in machine learning applications, can be expressed naturally in Haskell using parallel combinators and evaluation strategies. These mechanisms provide fine-grained control over computational resource utilization while maintaining the mathematical properties and referential transparency that characterize functional programming.
Distributed machine learning algorithms, such as parameter servers and federated learning systems, benefit from Haskell’s compositional approach to concurrent programming. The mathematical foundations ensure that distributed computations maintain consistency and correctness properties while providing the scalability required for modern machine learning applications.
Testing and Verification of ML Algorithms
The mathematical nature of Haskell programming provides exceptional opportunities for testing and verification of machine learning algorithms through property-based testing and formal verification techniques. QuickCheck and similar property-based testing frameworks enable developers to specify mathematical properties that algorithms should satisfy and automatically generate test cases that explore the algorithmic behavior space comprehensively.
Mathematical properties such as convergence guarantees, invariant preservation, and algorithmic correctness can be expressed directly as testable properties, providing confidence in implementation quality that goes far beyond traditional unit testing approaches. This mathematical approach to testing is particularly valuable for machine learning applications where subtle algorithmic errors can be difficult to detect through conventional testing methodologies.
Formal verification techniques, enabled by Haskell’s mathematical foundations, provide ultimate assurance of algorithmic correctness for critical machine learning applications. The ability to prove mathematical properties of algorithms at compile time represents a significant advancement over testing-based approaches to quality assurance in machine learning software.
Integration with Mathematical Libraries
The Haskell ecosystem provides extensive libraries for mathematical computation that integrate seamlessly with functional machine learning implementations. Libraries such as HMatrix for linear algebra, Statistics for statistical computations, and various automatic differentiation packages provide efficient implementations of fundamental mathematical operations while maintaining the mathematical transparency and safety characteristics of functional programming.
Foreign function interfaces enable integration with optimized numerical libraries such as BLAS and LAPACK when computational performance requirements demand the efficiency of carefully tuned imperative implementations. This hybrid approach allows developers to benefit from both the mathematical elegance of functional programming and the computational efficiency of specialized numerical libraries.
The mathematical consistency between different libraries in the Haskell ecosystem ensures that complex machine learning applications can be constructed by composing components from multiple sources without compromising mathematical correctness or introducing subtle incompatibilities that might affect algorithmic behavior.

The quantitative comparison between functional and imperative approaches to machine learning development reveals significant advantages in mathematical correctness, type safety, and code maintainability when using functional programming paradigms, though traditional imperative approaches may retain advantages in raw performance optimization and initial learning accessibility.
Real-World Applications and Case Studies
Despite its academic reputation, Haskell has been successfully applied to numerous real-world machine learning problems where mathematical rigor and safety are paramount. Financial modeling applications benefit from Haskell’s mathematical approach to quantitative analysis and risk assessment, where the consequences of algorithmic errors can be severe and mathematical correctness is essential.
Scientific computing applications, particularly those involving complex mathematical simulations and data analysis pipelines, leverage Haskell’s mathematical programming capabilities to ensure reproducibility and correctness of research results. The mathematical transparency of functional implementations facilitates peer review and scientific validation processes that are crucial for research integrity.
Industrial applications of Haskell in machine learning include compiler optimization, program analysis, and verification systems where the mathematical foundations of functional programming provide natural frameworks for reasoning about complex computational systems. These applications demonstrate that Haskell’s mathematical approach to programming can be both practical and performant in demanding real-world scenarios.
Future Directions in Functional AI
The future of functional artificial intelligence programming promises continued evolution toward more sophisticated mathematical abstractions and more powerful type systems that can encode increasingly complex mathematical relationships and constraints. Dependent type systems and proof assistants are likely to play growing roles in ensuring mathematical correctness of machine learning implementations while maintaining practical usability for everyday programming tasks.
Category theory and other advanced mathematical frameworks are beginning to influence the design of functional programming languages and libraries, providing new abstraction mechanisms that could revolutionize how machine learning algorithms are conceived and implemented. These mathematical foundations offer potential for unprecedented levels of abstraction and composability in AI system design.
The integration of formal methods and machine learning represents an emerging frontier where Haskell’s mathematical programming capabilities could enable new approaches to verifiable AI systems that provide mathematical guarantees about their behavior and performance characteristics. This convergence of formal verification and machine learning could address growing concerns about AI safety and reliability in critical applications.
The mathematical elegance and safety guarantees provided by functional programming approaches to machine learning represent a compelling alternative to conventional imperative methodologies, offering benefits in correctness, maintainability, and mathematical transparency that become increasingly valuable as AI systems grow in complexity and importance. The future of AI development may well depend on embracing these mathematical foundations that functional programming languages like Haskell provide so elegantly.
Disclaimer
This article is for informational purposes only and does not constitute professional advice. The views expressed are based on current understanding of functional programming methodologies and their applications in machine learning development. Readers should conduct their own research and consider their specific requirements when choosing programming approaches for machine learning projects. The effectiveness of functional programming techniques may vary depending on specific use cases, performance requirements, and development constraints.
