The foundation of reliable machine learning systems rests upon rigorous model validation methodologies that ensure predictive accuracy, generalizability, and robust performance across diverse datasets. Among the most critical decisions facing data scientists and machine learning engineers is the selection of appropriate validation strategies, with cross-validation and holdout testing representing the two predominant approaches that fundamentally shape how models are evaluated, refined, and ultimately deployed in production environments.
Explore the latest AI and machine learning trends to understand how validation techniques are evolving alongside advancing algorithmic capabilities. The choice between different validation methodologies can significantly impact model performance assessment, computational efficiency, and the reliability of performance metrics that guide critical business decisions and scientific conclusions.
Understanding Model Validation Fundamentals
Model validation serves as the cornerstone of machine learning methodology, providing essential mechanisms for assessing how well trained models generalize to unseen data and perform in real-world scenarios. The primary objective of validation is to estimate the true error rate of a model when applied to independent datasets that were not used during the training process, thereby preventing overfitting and ensuring that model performance metrics accurately reflect expected behavior in production environments.
The validation process involves partitioning available data into distinct subsets that serve different purposes throughout the model development lifecycle. Training data is used to fit model parameters and learn underlying patterns, validation data guides hyperparameter tuning and model selection decisions, and test data provides final, unbiased performance estimates that simulate real-world deployment conditions. This systematic separation of data ensures that model evaluation remains objective and that performance metrics genuinely reflect the model’s ability to handle previously unseen information.
Effective validation strategies must balance multiple competing objectives including computational efficiency, statistical reliability, and practical implementation constraints. The choice of validation methodology depends on various factors including dataset size, computational resources, model complexity, and the specific requirements of the application domain. Understanding these trade-offs is essential for selecting validation approaches that provide meaningful insights while remaining feasible within project constraints.
Cross-Validation: Maximizing Data Utilization
Cross-validation represents a sophisticated approach to model validation that maximizes the utilization of available data by systematically partitioning the dataset into multiple folds and iteratively using different combinations of these folds for training and validation purposes. The most common implementation, k-fold cross-validation, divides the dataset into k equal-sized subsets, trains the model k times using k-1 folds for training and the remaining fold for validation, then aggregates the results to produce robust performance estimates.
The fundamental advantage of cross-validation lies in its ability to provide comprehensive performance assessment using the entire dataset, thereby generating more reliable estimates of model performance compared to single train-validation splits. Each data point serves as both training and validation data across different iterations, ensuring that performance metrics reflect the model’s behavior across diverse data configurations and reducing the impact of particular data partitions on validation results.
Enhance your machine learning projects with Claude’s advanced analytical capabilities to implement sophisticated validation strategies that ensure robust model performance across diverse datasets. The iterative nature of cross-validation provides valuable insights into model stability and consistency, revealing whether performance varies significantly across different data subsets and helping identify potential issues with model generalization.
Implementing K-Fold Cross-Validation Strategies
K-fold cross-validation implementation involves careful consideration of fold selection, stratification strategies, and performance aggregation methodologies. The choice of k typically ranges from 5 to 10, with 10-fold cross-validation being widely adopted due to its balance between computational efficiency and statistical reliability. Smaller values of k reduce computational requirements but may produce less stable performance estimates, while larger values increase computational cost but provide more thorough validation coverage.
Stratified cross-validation represents an important variant that ensures proportional representation of different classes or target value ranges within each fold, particularly crucial for imbalanced datasets where random partitioning might create folds with significantly different class distributions. This approach maintains the original dataset’s statistical properties across all folds, ensuring that validation results accurately reflect model performance across all target categories.
The aggregation of results across cross-validation folds requires careful statistical consideration, with mean performance metrics providing central tendency measures and standard deviations indicating performance variability. These statistics enable comprehensive model assessment that considers both average performance and consistency across different data partitions, supporting informed decisions about model reliability and deployment readiness.
Leave-One-Out and Specialized Cross-Validation Variants
Leave-one-out cross-validation represents the extreme case where k equals the number of data points in the dataset, creating the maximum possible number of training iterations with each iteration excluding only a single observation for validation. This approach provides the most comprehensive data utilization possible but becomes computationally prohibitive for large datasets due to the extensive number of model training iterations required.
Time series cross-validation addresses the unique challenges posed by temporal data where traditional random partitioning violates the temporal ordering that is fundamental to accurate forecasting. This specialized approach uses expanding or rolling windows that respect chronological sequences, ensuring that models are always trained on historical data and validated on future observations, thereby maintaining the realistic temporal dynamics that characterize time series prediction scenarios.
Group-based cross-validation addresses situations where data points are naturally clustered into groups that should not be split across training and validation sets, such as medical data from individual patients or financial data from specific institutions. This approach ensures that validation results accurately reflect the model’s ability to generalize to entirely new groups rather than merely new observations from previously seen groups.

The diverse cross-validation methodologies each offer unique advantages and limitations that make them suitable for different types of machine learning problems. Understanding these distinctions enables data scientists to select validation approaches that align with their specific dataset characteristics and modeling objectives.
Holdout Testing: Simplicity and Efficiency
Holdout testing provides a straightforward validation approach that divides the available dataset into distinct training and testing subsets, typically using random sampling to ensure representative distribution of data characteristics across both partitions. The most common implementation allocates approximately 70-80% of data for training and reserves 20-30% for testing, though these proportions may be adjusted based on dataset size and specific project requirements.
The primary advantage of holdout testing lies in its computational efficiency and conceptual simplicity, making it particularly attractive for large datasets where cross-validation would be computationally prohibitive or for rapid prototyping scenarios where quick performance estimates are needed. The single train-test split requires only one model training iteration, significantly reducing computational requirements compared to cross-validation approaches that necessitate multiple training cycles.
Holdout testing closely mirrors real-world deployment scenarios where models are trained on historical data and applied to new, incoming observations. This alignment with practical implementation contexts makes holdout validation results particularly relevant for assessing expected production performance, provided that the test set remains truly representative of future data distributions.
Strategic Data Splitting for Holdout Validation
Effective holdout validation requires careful consideration of data splitting strategies that ensure representative sampling while maintaining statistical validity. Random sampling forms the foundation of most holdout implementations, but stratified sampling may be necessary for imbalanced datasets to ensure adequate representation of minority classes in both training and testing subsets.
The temporal dimension adds complexity to holdout validation for time series data, where chronological ordering must be preserved to maintain realistic validation conditions. Temporal splitting typically assigns earlier observations to training sets and later observations to test sets, ensuring that models are evaluated on genuinely future data rather than randomly selected contemporaneous observations.
The proportion of data allocated to training versus testing involves trade-offs between model performance and validation reliability. Larger training sets enable better model learning but provide less data for performance assessment, while larger test sets improve validation reliability but may compromise model training quality. These decisions must be balanced against dataset size, model complexity, and the specific requirements of the application domain.
Three-Way Data Splitting and Validation Sets
Advanced holdout strategies implement three-way data splitting that creates distinct training, validation, and test sets to support comprehensive model development workflows. The validation set serves as an intermediate evaluation dataset used for hyperparameter tuning, model selection, and early stopping decisions, while the test set remains completely isolated until final performance assessment.
This three-way approach prevents information leakage from the test set during model development, ensuring that final performance estimates remain unbiased and genuinely reflect expected performance on unseen data. The validation set enables iterative model refinement without compromising the integrity of the final evaluation, supporting systematic optimization of model architecture and hyperparameters.
The allocation of data across training, validation, and test sets typically follows proportions such as 60-20-20 or 70-15-15, depending on dataset size and model complexity requirements. Smaller datasets may require different proportions to ensure adequate data for each purpose, while larger datasets provide more flexibility in allocation strategies.
Utilize Perplexity’s research capabilities to stay updated on the latest developments in model validation methodologies and best practices that are emerging from the machine learning research community. The field continues to evolve with new techniques that address specific validation challenges in diverse application domains.
Comparing Cross-Validation and Holdout Performance
The fundamental trade-off between cross-validation and holdout testing centers on the balance between computational cost and statistical reliability. Cross-validation provides more robust performance estimates by utilizing the entire dataset for both training and validation, reducing the variance in performance metrics that can result from particular data partitions. However, this comprehensive approach requires multiple model training iterations that significantly increase computational requirements.
Holdout testing offers computational efficiency and practical alignment with deployment scenarios, making it particularly suitable for large-scale applications where cross-validation would be computationally prohibitive. The simplicity of holdout approaches also facilitates easier implementation and interpretation, particularly in production environments where validation processes must be integrated into automated pipelines and monitoring systems.
The statistical properties of performance estimates differ significantly between the two approaches. Cross-validation typically produces performance estimates with lower variance due to the averaging effect across multiple folds, while holdout estimates may exhibit higher variance depending on the particular train-test split selected. However, cross-validation estimates may exhibit slight bias due to the overlap in training sets across different folds.
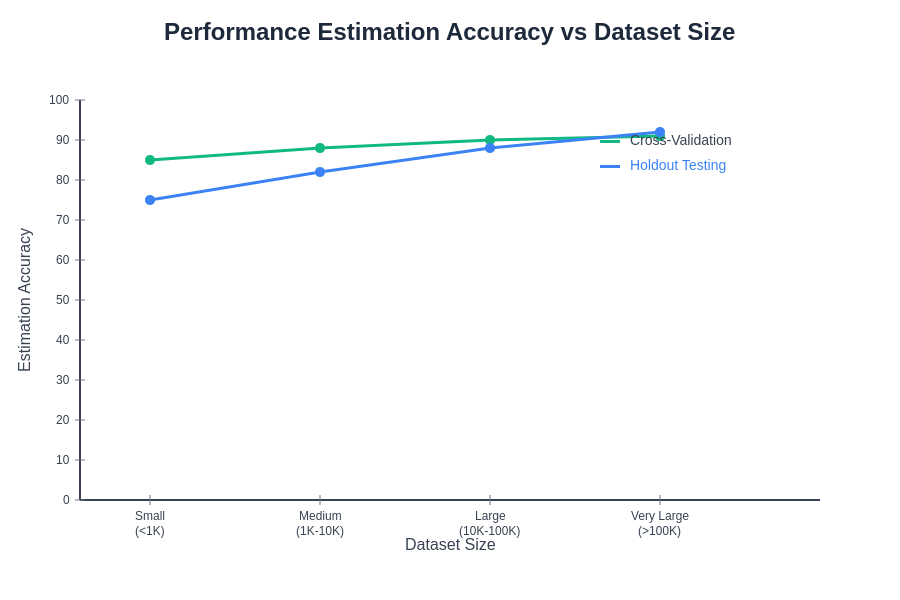
The accuracy and reliability of performance estimates vary significantly between cross-validation and holdout methods depending on dataset characteristics, model complexity, and implementation details. Understanding these differences is crucial for selecting validation strategies that provide meaningful insights for specific machine learning applications.
Dataset Size Considerations and Validation Strategy Selection
Dataset size plays a crucial role in determining the optimal validation strategy, with different approaches being more suitable for small, medium, and large datasets. Small datasets benefit significantly from cross-validation approaches that maximize data utilization, as holdout testing may not provide sufficient data for reliable training or testing. The comprehensive data usage in cross-validation becomes particularly valuable when every available observation contributes to model performance assessment.
Medium-sized datasets provide flexibility in validation strategy selection, with both cross-validation and holdout approaches being viable depending on computational constraints and performance requirements. The decision often depends on factors such as model complexity, available computational resources, and the specific performance metrics that are most important for the application domain.
Large datasets may favor holdout approaches due to computational efficiency considerations, particularly when the test set size remains sufficiently large to provide reliable performance estimates. The abundance of data in large datasets reduces the statistical advantages of cross-validation while the computational costs become increasingly prohibitive for complex models that require significant training time.
Temporal Data and Sequential Validation Challenges
Time series data introduces unique validation challenges that require specialized approaches to maintain temporal integrity and provide realistic performance assessment. Traditional cross-validation methods that randomly partition data violate the chronological ordering that is fundamental to time series modeling, potentially leading to data leakage where future information influences predictions about past events.
Temporal validation strategies must ensure that models are always trained on historical data and validated on future observations, maintaining the causal relationships that characterize real-world forecasting scenarios. This requirement necessitates specialized cross-validation variants such as time series split validation or expanding window approaches that respect temporal ordering while still providing comprehensive model assessment.
The selection of validation windows for temporal data involves considerations of seasonality, trend patterns, and the specific forecasting horizon that the model will be used for in production. Validation periods should be representative of the time scales and patterns that the model will encounter during deployment, ensuring that performance estimates accurately reflect expected operational behavior.
Computational Resource Optimization
The computational requirements of different validation strategies vary dramatically and must be considered when selecting appropriate methodologies for specific applications. Cross-validation requires k times the computational resources of holdout testing due to the multiple training iterations, making it potentially prohibitive for complex models or large datasets with limited computational budgets.
Modern distributed computing environments and cloud platforms provide opportunities to parallelize cross-validation computations across multiple processing units, potentially reducing the wall-clock time required for comprehensive validation. However, the total computational cost remains proportionally higher, and resource allocation decisions must balance validation thoroughness against available computational budgets.
Approximation techniques such as subsampling or early stopping can reduce the computational requirements of cross-validation while maintaining much of the statistical benefit. These hybrid approaches provide middle-ground solutions that offer improved reliability compared to simple holdout testing while remaining computationally tractable for resource-constrained environments.
Statistical Significance and Confidence Intervals
The statistical interpretation of validation results requires careful consideration of confidence intervals, significance testing, and the underlying assumptions of different validation methodologies. Cross-validation provides multiple performance estimates that enable statistical testing of model differences and calculation of confidence intervals around performance metrics, supporting more rigorous model comparison and selection processes.
Holdout testing produces single point estimates of performance that provide limited information about the uncertainty associated with these measurements. While bootstrap resampling can be applied to holdout results to estimate confidence intervals, this approach requires additional computational overhead that reduces some of the efficiency advantages of holdout testing.
The interpretation of performance differences between models depends on the validation methodology employed, with cross-validation providing more robust frameworks for statistical significance testing. Paired statistical tests can be applied to cross-validation results to determine whether observed performance differences are statistically significant or could reasonably be attributed to random variation.
Industry Applications and Best Practices
Different industries and application domains have developed specialized best practices for model validation that reflect the unique requirements and constraints of their specific contexts. Financial services applications often require regulatory compliance that mandates particular validation approaches and documentation standards, influencing the choice between cross-validation and holdout methods based on auditing and interpretability requirements.
Healthcare applications must balance validation thoroughness with patient privacy considerations and regulatory requirements that may restrict data usage patterns. The life-critical nature of many medical applications often favors more conservative validation approaches that provide comprehensive performance assessment even at the cost of increased computational requirements.
Technology companies operating at scale may prioritize computational efficiency and practical alignment with deployment scenarios, leading to preference for holdout testing approaches that can be easily integrated into automated model development pipelines. The ability to quickly iterate and validate models becomes particularly important in rapidly evolving competitive environments.
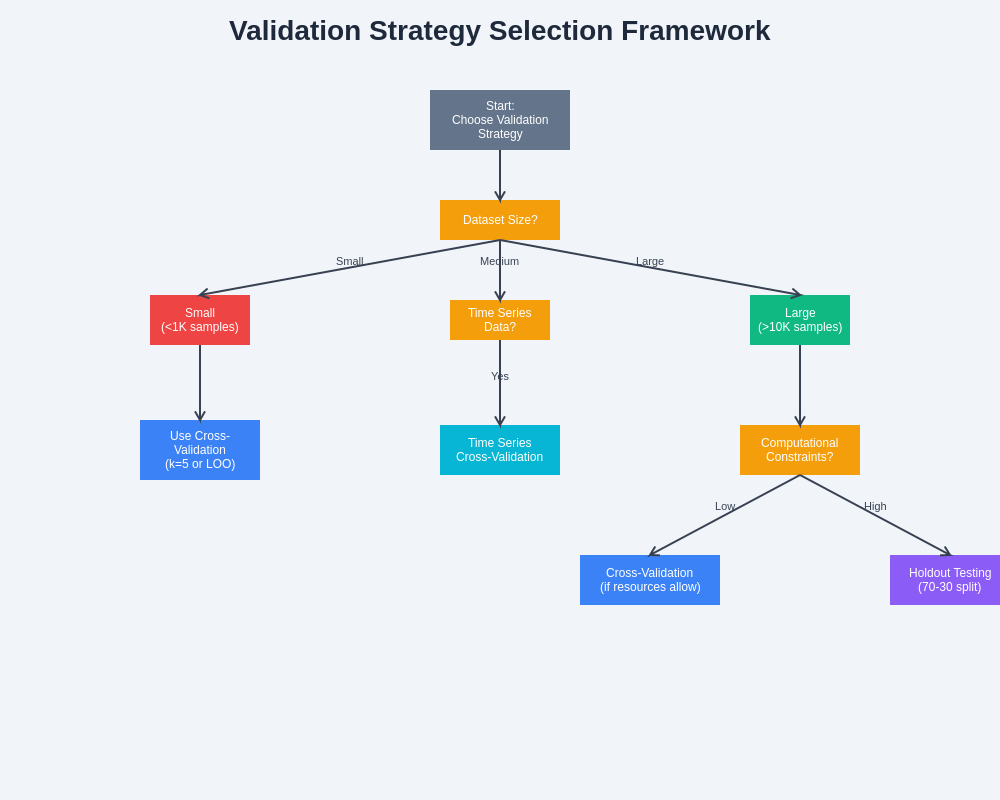
The selection of appropriate validation strategies requires systematic consideration of multiple factors including dataset characteristics, computational constraints, statistical requirements, and domain-specific considerations that influence the trade-offs between different approaches.
Future Directions and Emerging Techniques
The field of model validation continues to evolve with new techniques that address specific limitations of traditional cross-validation and holdout approaches. Nested cross-validation provides frameworks for simultaneously optimizing hyperparameters and estimating performance while maintaining statistical validity, though at the cost of increased computational complexity.
Advanced resampling techniques such as bootstrap aggregation and permutation testing offer alternative approaches to performance estimation that may be more appropriate for certain types of data distributions or model architectures. These methods provide different statistical properties compared to traditional validation approaches and may offer advantages in specific application contexts.
The integration of validation strategies with modern machine learning pipelines and automated model development workflows continues to drive innovation in practical validation implementations. Tools and frameworks that seamlessly integrate validation processes with model training, hyperparameter optimization, and deployment pipelines are becoming increasingly important for operational machine learning systems.
The emergence of federated learning, privacy-preserving machine learning, and other distributed training paradigms introduces new validation challenges that require novel approaches to ensure model performance assessment while respecting privacy and security constraints. These evolving requirements are driving research into validation methodologies that can operate effectively in distributed and privacy-constrained environments.
Conclusion and Strategic Recommendations
The choice between cross-validation and holdout testing strategies represents a fundamental decision in machine learning model development that significantly impacts the reliability of performance estimates, computational efficiency, and practical implementation considerations. Cross-validation provides more robust statistical properties and comprehensive data utilization, making it particularly valuable for smaller datasets and scenarios where thorough performance assessment is critical.
Holdout testing offers computational efficiency and practical alignment with deployment scenarios, making it suitable for large-scale applications where cross-validation would be prohibitively expensive or for rapid prototyping where quick performance estimates are needed. The decision between these approaches should consider dataset size, computational resources, statistical requirements, and the specific constraints of the application domain.
The most effective validation strategies often combine elements of both approaches, using cross-validation for comprehensive model development and holdout testing for final performance confirmation. This hybrid approach leverages the statistical advantages of cross-validation while maintaining the practical benefits and computational efficiency of holdout validation for final model assessment.
Disclaimer
This article is for informational purposes only and does not constitute professional advice. The views expressed are based on current understanding of machine learning validation techniques and their applications. Readers should conduct their own research and consider their specific requirements when implementing model validation strategies. The effectiveness of validation approaches may vary depending on specific use cases, dataset characteristics, and modeling objectives.
