The convergence of quantum computing and artificial intelligence has ushered in a revolutionary era for financial risk modeling, fundamentally transforming how institutions approach portfolio optimization, market prediction, and risk assessment. This groundbreaking intersection of quantum mechanics, advanced computing, and financial mathematics represents one of the most significant technological advances in quantitative finance, promising to solve previously intractable computational problems that have long challenged traditional financial modeling approaches.
Discover the latest AI developments in finance as quantum computing continues to reshape the financial technology landscape with unprecedented computational capabilities. The emergence of quantum finance AI represents not merely an incremental improvement in existing methodologies, but a paradigmatic shift that enables financial institutions to process vast amounts of market data, optimize complex portfolios, and model intricate risk scenarios with unprecedented speed and accuracy.
The Quantum Advantage in Financial Computing
Quantum computing brings fundamental advantages to financial risk modeling through its ability to process exponentially larger datasets and perform parallel computations that would be impossible with classical computers. The quantum properties of superposition and entanglement allow quantum systems to explore multiple solution paths simultaneously, making them particularly well-suited for solving the complex optimization problems that are central to modern financial risk management.
Traditional risk modeling approaches often rely on Monte Carlo simulations and other classical computational methods that require significant approximations when dealing with large portfolios or complex derivatives. Quantum algorithms can potentially reduce the computational complexity of these problems from exponential to polynomial time, enabling real-time risk assessment for portfolios containing thousands of assets and complex interdependencies that would overwhelm classical systems.
The quantum advantage becomes particularly pronounced when dealing with high-dimensional optimization problems common in portfolio management, where the number of possible combinations grows exponentially with the number of assets. Quantum annealing and variational quantum algorithms can explore these vast solution spaces more efficiently, identifying optimal portfolio allocations that maximize returns while minimizing risk exposure across multiple market scenarios.
Quantum Machine Learning for Market Prediction
The integration of quantum computing with machine learning algorithms has opened new frontiers in market prediction and trend analysis. Quantum machine learning leverages the probabilistic nature of quantum systems to enhance pattern recognition in financial data, potentially identifying subtle market signals that classical algorithms might miss. These quantum-enhanced models can process larger feature spaces and identify complex correlations between seemingly unrelated market variables.
Quantum neural networks and quantum support vector machines represent particularly promising approaches for analyzing market volatility and predicting price movements. These algorithms can capture non-linear relationships in financial data more effectively than their classical counterparts, potentially improving the accuracy of risk predictions and enabling more sophisticated hedging strategies. The quantum approach to feature mapping allows for the representation of financial data in higher-dimensional spaces, where previously hidden patterns may become apparent.
Enhance your AI capabilities with Claude to explore advanced quantum computing concepts and their applications in financial modeling with cutting-edge analytical support. The combination of quantum computing and artificial intelligence creates unprecedented opportunities for developing sophisticated risk models that can adapt to changing market conditions and identify emerging threats before they materialize.
Advanced Portfolio Optimization Techniques
Quantum computing has revolutionized portfolio optimization by enabling the solution of previously intractable problems involving large numbers of assets and complex constraints. The Quantum Approximate Optimization Algorithm (QAOA) and other quantum heuristics can efficiently navigate the vast solution space of portfolio optimization problems, finding optimal or near-optimal asset allocations that balance risk and return across multiple market scenarios.
These quantum approaches excel at handling the non-convex optimization problems that arise in real-world portfolio management, where traditional linear programming methods fall short. Quantum algorithms can simultaneously consider multiple risk factors, correlation structures, and market constraints while optimizing for various objectives such as maximum Sharpe ratio, minimum variance, or maximum diversification. The ability to incorporate dynamic rebalancing strategies and transaction costs into the optimization process makes quantum portfolio optimization particularly valuable for practical applications.
The quantum approach also enables more sophisticated risk budgeting techniques, where risk allocation across different asset classes and investment strategies can be optimized in real-time. This capability is particularly valuable for institutional investors managing complex portfolios with multiple layers of risk factors and regulatory constraints that must be satisfied simultaneously.
Quantum Risk Measurement and VaR Calculations
Value at Risk (VaR) calculations represent one of the most computationally intensive aspects of financial risk management, particularly for large portfolios with complex derivatives and non-linear exposures. Quantum computing offers significant advantages for these calculations through quantum Monte Carlo methods that can achieve quadratic speedups over classical approaches while maintaining or improving accuracy levels.
Quantum algorithms for VaR calculation can handle the high-dimensional integration problems that arise when modeling portfolio risk across multiple market factors and time horizons. The quantum Fourier transform and other quantum algorithms enable more efficient sampling of extreme market scenarios, improving the statistical reliability of tail risk estimates. This enhanced capability is particularly crucial for stress testing and regulatory capital calculations, where accurate estimation of extreme losses is essential for financial stability.
The quantum approach also enables more sophisticated coherent risk measures beyond traditional VaR, including Expected Shortfall and spectral risk measures that provide a more complete picture of portfolio risk. These advanced risk metrics can be computed more efficiently using quantum algorithms, enabling real-time risk monitoring and dynamic hedging strategies that adapt to changing market conditions.
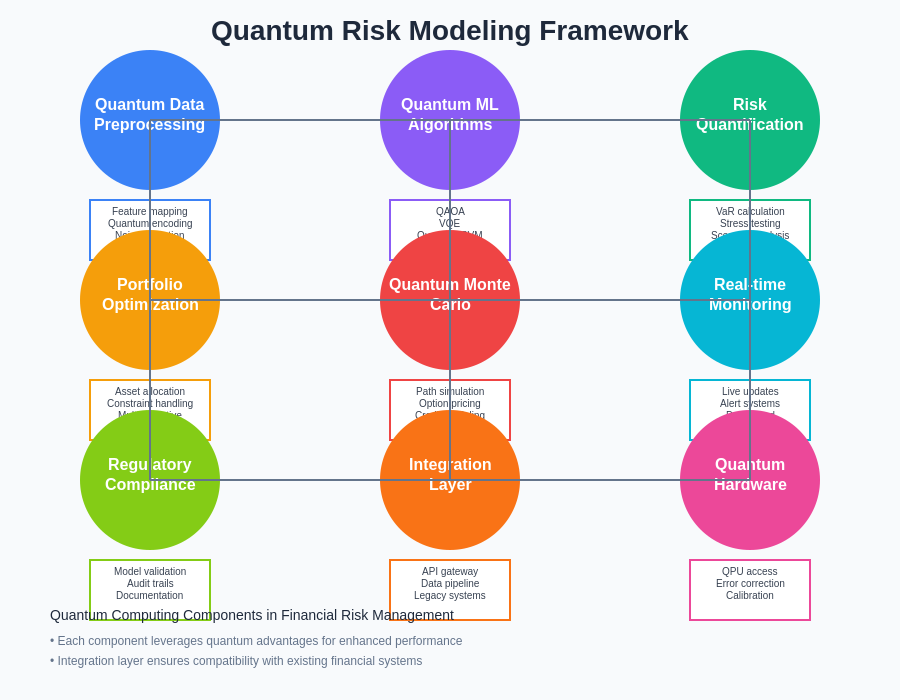
The quantum risk modeling framework integrates multiple quantum algorithms and computational techniques to create a comprehensive approach to financial risk assessment. This systematic methodology leverages quantum advantages at each stage of the risk modeling process, from data preprocessing and feature extraction to optimization and scenario analysis.
Quantum Credit Risk Models
Credit risk modeling has been transformed through quantum computing applications that can analyze vast networks of interconnected counterparties and complex credit derivatives. Quantum algorithms excel at modeling the systemic risk that emerges from the interconnected nature of modern financial systems, where the failure of one institution can cascade through the network and create widespread instability.
Quantum graph algorithms can efficiently analyze credit networks and identify critical nodes whose failure would have the greatest systemic impact. These algorithms can process network structures with thousands of nodes and millions of connections, enabling comprehensive stress testing of the entire financial system. The quantum approach to network analysis reveals hidden vulnerabilities and concentration risks that might not be apparent through traditional methods.
Machine learning models enhanced with quantum computing can improve credit scoring and default prediction by analyzing larger datasets and identifying complex patterns in borrower behavior. Quantum feature mapping enables the representation of credit data in higher-dimensional spaces where linear separability of good and bad credits may be achieved more easily. This enhanced analytical capability can lead to more accurate credit decisions and better pricing of credit risk across different market segments.
Derivatives Pricing with Quantum Algorithms
The pricing of complex derivatives represents one of the most computationally challenging problems in quantitative finance, particularly for path-dependent options, exotic derivatives, and structured products with multiple underlying assets. Quantum computing offers significant advantages for these calculations through quantum algorithms that can efficiently handle the high-dimensional integration problems inherent in derivatives pricing.
Quantum Monte Carlo methods can achieve quadratic speedups for option pricing calculations while maintaining high accuracy levels. This improvement is particularly valuable for pricing complex derivatives that require extensive simulation of underlying asset paths, such as American options, barrier options, and multi-asset derivatives. The quantum advantage becomes more pronounced as the number of underlying assets and the complexity of the payoff structure increase.
The quantum approach also enables more sophisticated model calibration procedures, where the parameters of pricing models can be optimized against market data more efficiently. Quantum optimization algorithms can simultaneously calibrate multiple model parameters while ensuring that the resulting model remains arbitrage-free and produces realistic market dynamics. This enhanced calibration capability leads to more accurate pricing and better risk management for derivatives portfolios.
Explore comprehensive AI research with Perplexity to stay updated on the latest developments in quantum finance and advanced risk modeling techniques that are shaping the future of financial technology. The rapid evolution of quantum computing capabilities continues to expand the possibilities for innovative financial applications and risk management strategies.
Quantum Stress Testing and Scenario Analysis
Stress testing represents a critical component of financial risk management that has been significantly enhanced through quantum computing capabilities. Traditional stress testing approaches are limited by computational constraints when modeling extreme market scenarios across large portfolios with complex interdependencies. Quantum algorithms can efficiently explore vast scenario spaces and identify the most critical stress scenarios that could impact portfolio performance.
Quantum simulation techniques enable more realistic modeling of market dynamics under extreme conditions, incorporating features such as volatility clustering, fat-tailed distributions, and regime changes that are difficult to capture with classical methods. These enhanced stress testing capabilities provide financial institutions with better insights into their vulnerability to systemic risks and extreme market events, enabling more effective risk management strategies.
The quantum approach to scenario generation can create more diverse and comprehensive stress scenarios that cover a wider range of potential market conditions. Quantum random number generators and quantum sampling techniques can produce scenario sets that better represent the true uncertainty in financial markets, leading to more robust stress testing results and better preparedness for unexpected market developments.
Real-Time Risk Monitoring Systems
The development of quantum-enhanced risk monitoring systems represents a significant advancement in real-time financial risk management. These systems leverage quantum computing’s parallel processing capabilities to continuously monitor portfolio risk across multiple dimensions and market conditions, providing immediate alerts when risk thresholds are exceeded or when market conditions suggest increased vulnerability to adverse events.
Quantum algorithms enable more sophisticated real-time correlation analysis, identifying subtle changes in asset relationships that might signal emerging risks or market instability. The ability to process high-frequency data streams and update risk models in real-time provides financial institutions with unprecedented visibility into their risk exposure and enables more responsive risk management strategies.
Machine learning models enhanced with quantum computing can adapt to changing market conditions more quickly than traditional models, improving the accuracy of real-time risk predictions. These adaptive models can identify emerging patterns in market data and adjust their risk assessments accordingly, providing early warning signals for potential market disruptions or portfolio losses.
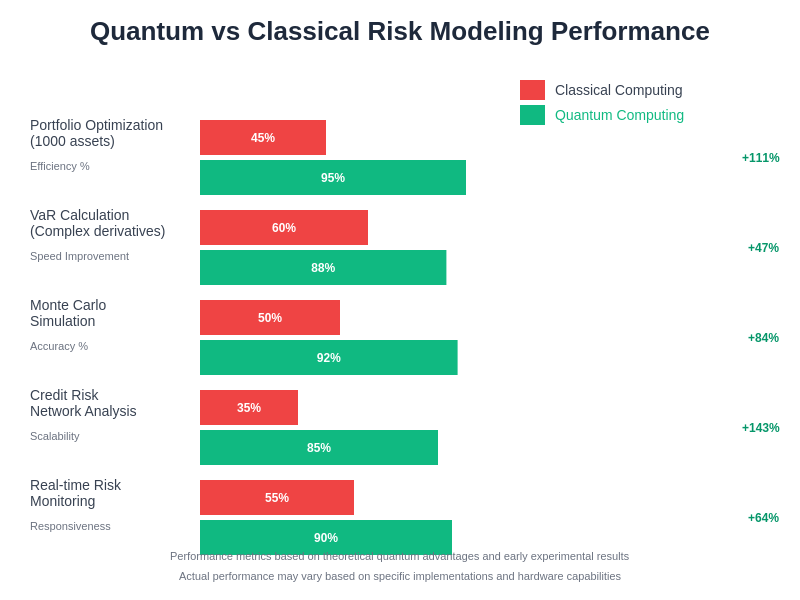
The performance advantages of quantum computing in financial risk modeling are substantial across multiple key metrics. Quantum algorithms demonstrate superior computational efficiency, accuracy, and scalability compared to classical approaches, particularly for complex optimization problems and high-dimensional risk calculations that are central to modern financial risk management.
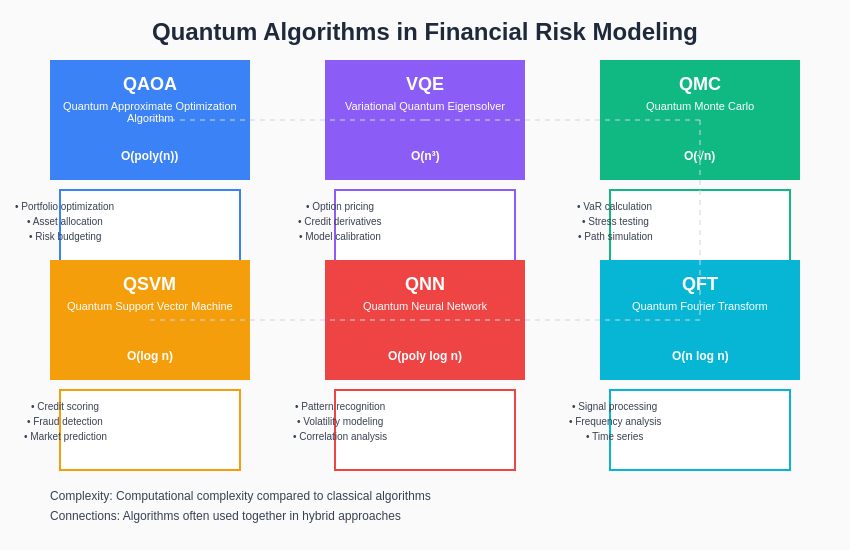
The diverse array of quantum algorithms available for financial applications each offers unique advantages for specific risk modeling challenges. From portfolio optimization using QAOA to credit risk analysis with quantum machine learning, these algorithms provide unprecedented computational capabilities that can transform traditional financial risk management approaches.
Regulatory Implications and Compliance
The adoption of quantum computing in financial risk modeling raises important questions about regulatory compliance and model validation that financial institutions must carefully consider. Regulatory frameworks are evolving to accommodate the unique characteristics of quantum algorithms while ensuring that risk models remain transparent, auditable, and reliable for regulatory capital calculations and stress testing requirements.
Model validation for quantum-based risk models presents unique challenges, as traditional backtesting and sensitivity analysis techniques may need to be adapted for quantum algorithms. Regulatory authorities are working to develop guidelines for the validation of quantum models while ensuring that the benefits of quantum computing can be realized without compromising financial stability or consumer protection.
The transparency and explainability of quantum models represent particular challenges for regulatory compliance, as quantum algorithms may produce accurate results through processes that are difficult to interpret using traditional analytical frameworks. Financial institutions must develop new approaches to model documentation and validation that can satisfy regulatory requirements while leveraging the full capabilities of quantum computing.
Implementation Challenges and Solutions
The practical implementation of quantum finance AI faces several significant challenges that must be addressed for successful deployment in production environments. Quantum hardware limitations, including limited qubit counts, short coherence times, and high error rates, currently constrain the complexity of problems that can be solved using existing quantum computers. However, rapid advances in quantum error correction and fault-tolerant quantum computing are steadily expanding the range of practical applications.
Software development for quantum finance applications requires specialized expertise that combines quantum computing knowledge with deep understanding of financial mathematics and risk modeling. The shortage of professionals with these interdisciplinary skills represents a significant barrier to widespread adoption, necessitating substantial investment in training and education programs.
Integration with existing financial systems and databases presents additional challenges, as quantum algorithms must interface with classical computing infrastructure and legacy risk management systems. Hybrid quantum-classical approaches that leverage the strengths of both computing paradigms offer promising solutions for overcoming these integration challenges while maximizing the benefits of quantum computing.
Future Developments and Market Impact
The future of quantum finance AI promises even more revolutionary developments as quantum hardware continues to improve and new algorithms are developed specifically for financial applications. The emergence of fault-tolerant quantum computers with hundreds or thousands of logical qubits will enable the solution of much larger and more complex risk modeling problems, potentially transforming the entire landscape of quantitative finance.
Advances in quantum machine learning are expected to yield even more sophisticated market prediction models that can identify subtle patterns and relationships in financial data that are invisible to classical analysis. These enhanced predictive capabilities could lead to more accurate risk models, better investment strategies, and more effective hedging techniques that provide superior risk-adjusted returns.
The democratization of quantum computing through cloud-based quantum services is expected to accelerate adoption across the financial industry, enabling smaller institutions to access quantum computing capabilities without massive capital investments. This broader access to quantum technology could level the playing field in financial markets and drive innovation across the entire industry.
Integration with Traditional Finance
The successful integration of quantum computing with traditional financial systems requires careful consideration of how quantum algorithms can complement and enhance existing risk management processes without disrupting established workflows. Hybrid approaches that use quantum computing for specific computational bottlenecks while maintaining classical systems for routine operations offer practical pathways for gradual adoption.
Legacy system integration presents both challenges and opportunities, as financial institutions must balance the benefits of quantum computing with the need to maintain operational continuity and regulatory compliance. Phased implementation strategies that gradually introduce quantum capabilities for specific use cases allow institutions to gain experience with quantum technology while minimizing operational risks.
The cultural and organizational changes required for quantum adoption extend beyond technical considerations to include training programs, risk management procedures, and governance frameworks that can effectively oversee quantum-based financial models. Successful implementation requires collaboration between quantum computing experts, financial professionals, and risk management specialists to ensure that quantum technology is deployed effectively and safely.
Conclusion and Strategic Implications
Quantum Finance AI represents a transformative force that is reshaping the landscape of financial risk modeling and quantitative analysis. The convergence of quantum computing and artificial intelligence creates unprecedented opportunities for solving complex financial problems that have long challenged traditional computational approaches. As quantum hardware continues to improve and new algorithms are developed, the practical applications of quantum finance will expand dramatically, potentially revolutionizing every aspect of financial risk management.
The strategic implications of quantum finance extend far beyond computational improvements to encompass fundamental changes in how financial institutions approach risk, investment, and market analysis. Organizations that successfully integrate quantum computing capabilities will likely gain significant competitive advantages through superior risk management, more accurate market predictions, and more efficient portfolio optimization. The quantum advantage in finance is not merely about faster computation, but about solving previously impossible problems and gaining insights that were inaccessible through classical methods.
The future of financial risk modeling will be defined by the intelligent integration of quantum computing, artificial intelligence, and traditional financial expertise. This convergence promises to unlock new levels of understanding about market dynamics, risk relationships, and investment opportunities while maintaining the rigorous standards of accuracy and reliability that are essential for financial stability and regulatory compliance.
Disclaimer
This article is for informational and educational purposes only and does not constitute financial, investment, or professional advice. The discussion of quantum computing applications in finance reflects current research and development trends but should not be interpreted as recommendations for specific investment strategies or risk management approaches. Readers should consult with qualified financial professionals and conduct their own research before implementing any quantum-based financial models or strategies. The effectiveness and practical applicability of quantum finance techniques may vary significantly depending on specific use cases, market conditions, and technological limitations.